Get step-by-step solutions to your math problems
Try Math Solver
Get step-by-step explanations
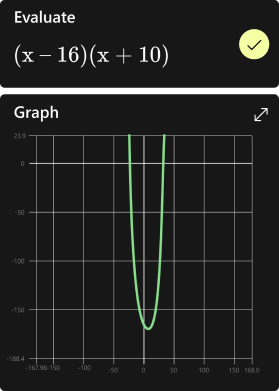
Graph your math problems
Practice, practice, practice
Get math help in your language
Math Solver
Geogebra math solver.
Get accurate solutions and step-by-step explanations for algebra and other math problems, while enhancing your problem-solving skills!
Step-by-Step Solutions
Use step-by-step calculators for chemistry, calculus, algebra, trigonometry, equation solving, basic math and more.
Gain more understanding of your homework with steps and hints guiding you from problems to answers! Wolfram|Alpha Pro step-by-step solutions not only give you the answers you're looking for, but also help you learn how to solve problems.
Starting at $ 5 .00 /month
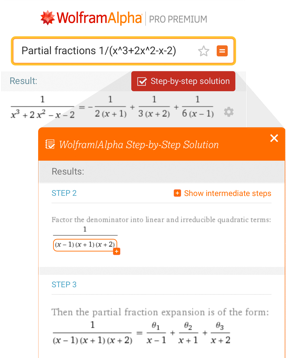
Step-by-Step Solutions Features
Not just answers—step-by-step solutions buttons expand answers and explain how that answer was found.
![[object Object]](https://www.wolframalpha.com/_next/static/images/sbs-solutions_2MB5WFCI.png "mathematics problem solving steps")
Show Intermediate Steps
Break steps down even further with intermediate steps. These optional additional explanations for individual pieces of step-by-step solutions help guide you.
![[object Object]](https://www.wolframalpha.com/_next/static/images/sbs-intermediate_NnfJanMv.png "mathematics problem solving steps")
Choose a Method
Explore different ways of finding a solution. Use your classroom's teaching method to guide you through the answer.
![[object Object]](https://www.wolframalpha.com/_next/static/images/sbs-methods_1EfrOjX1.png "mathematics problem solving steps")
Your own tutor—hints are also frequently provided to not just provide answers, but also to guide you towards finding the solution yourself.
![[object Object]](https://www.wolframalpha.com/_next/static/images/sbs-hints_Ru_Wwd42.png "mathematics problem solving steps")
Examples of Step-by-Step Solutions
Explore some of the content areas covered by step-by-step solutions, including math, chemistry and physics, or view more examples »
Equation Solving
More Math Topics
- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
The equations section of QuickMath allows you to solve and plot virtually any equation or system of equations. In most cases, you can find exact solutions to your equations. Even when this is not possible, QuickMath may be able to give you approximate solutions to almost any level of accuracy you require. It also contains a number of special commands for dealing with quadratic equations.
The Solve command can be uses to solve either a single equation for a single unknown from the basic solve page or to simultaneously solve a system of many equations in many unknowns from the advanced solve page . The advanced command allows you to specify whether you want approximate numerical answers as well as exact ones, and how many digits of accuracy (up to 16) you require. It also allows you to eliminate certain variables from the equations.
Go to the Solve page
The Plot command, from the Graphs section, will plot any function of two variables. In order to plot a single function of x, go to the basic equation plotting page , where you can enter the equation and specify the upper and lower limits on x that you want the graph to be plotted for. The advanced plotting page allows you to plot up to 6 equations on the one graph, each with their own color. It also gives you control over such things as whether or not to show the axes, where the axes should be located, what the aspect ratio of the plot should be and what the range of the dependent variable should be. All equations can be given in the explicit y = f(x) form or the implicit g(x,y) = c form.
Go to the Equation Plotting page
The Quadratics page contains 13 separate commands for dealing with the most common questions concerning quadratics. It allows you to : factor a quadratic function (by two different methods); solve a quadratic equation by factoring the quadratic, using the quadratic formula or by completing the square; rewrite a quadratic function in a different form by completing the square; calculate the concavity, x-intercepts, y-intercept, axis of symmetry and vertex of a parabola; plot a parabola; calculate the discriminant of a quadratic equation and use the discriminant to find the number of roots of a quadratic equation. Each command generates a complete and detailed custom-made explanation of all the steps needed to solve the problem.
Go to the Quadratics page
Introduction to Equations
By an equation we mean a mathematical sentence that states that two algebraic expressions are equal. For example, a (b + c) =ab + ac, ab = ba, and x 2 -1 = (x-1)(x+1) are all equations that we have been using. We recall that we defined a variable as a letter that may be replaced by numbers out of a given set, during a given discussion. This specified set of numbers is sometimes called the replacement set. In this chapter we will deal with equations involving variables where the replacement set, unless otherwise specified, is the set of all real numbers for which all the expressions in the equation are defined.
If an equation is true after the variable has been replaced by a specific number, then the number is called a solution of the equation and is said to satisfy it. Obviously, every solution is a member of the replacement set. The real number 3 is a solution of the equation 2x-1 = x+2, since 2*3-1=3+2. while 1 is a solution of the equation (x-1)(x+2) = 0. The set of all solutions of an equation is called the solution set of the equation.
In the first equation above {3} is the solution set, while in the second example {-2,1} is the solution set. We can verify by substitution that each of these numbers is a solution of its respective equation, and we will see later that these are the only solutions.
A conditional equation is an equation that is satisfied by some numbers from its replacement set and not satisfied by others. An identity is an equation that is satisfied by all numbers from its replacement set.
Example 1 Consider the equation 2x-1 = x+2
The replacement set here is the set of all real numbers. The equation is conditional since, for example, 1 is a member of the replacement set but not of the solution set.
Example 2 Consider the equation (x-1)(x+1) =x 2 -1 The replacement set is the set of all real numbers. From our laws of real numbers if a is any real number, then (a-1)(a+1) = a 2 -1 Therefore, every member of the replacement set is also a member of the solution set. Consequently this equation is an identity.
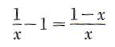
The replacement set for this equation is the set of real numbers except 0, since 1/x and (1- x)/x are not defined for x = 0. If a is any real number in the replacement set, then
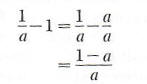
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth
20 Effective Math Strategies To Approach Problem-Solving
Katie Keeton
Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.
Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.
This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations.
What are problem-solving strategies?
Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies:
- Draw a model
- Use different approaches
- Check the inverse to make sure the answer is correct
Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better.
Strategies can help guide students to the solution when it is difficult ot know when to start.
The ultimate guide to problem solving techniques
Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.
20 Math Strategies For Problem-Solving
Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem.
Here are 20 strategies to help students develop their problem-solving skills.
Strategies to understand the problem
Strategies that help students understand the problem before solving it helps ensure they understand:
- The context
- What the key information is
- How to form a plan to solve it
Following these steps leads students to the correct solution and makes the math word problem easier .
Here are five strategies to help students understand the content of the problem and identify key information.
1. Read the problem aloud
Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.
2. Highlight keywords
When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed. For example, if the word problem asks how many are left, the problem likely requires subtraction. Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.
3. Summarize the information
Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary. Summaries should include only the important information and be in simple terms that help contextualize the problem.
4. Determine the unknown
A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer. Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.
5. Make a plan
Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it. The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer. Encourage students to make a list of each step they need to take to solve the problem before getting started.
Strategies for solving the problem
1. draw a model or diagram.
Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process. It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.
Similarly, you could draw a model to represent the objects in the problem:
2. Act it out
This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives . When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts. The examples below show how 1st-grade students could “act out” an addition and subtraction problem:
| The problem | How to act out the problem |
| Gia has 6 apples. Jordan has 3 apples. How many apples do they have altogether? | Two students use counters to represent the apples. One student has 6 counters and the other student takes 3. Then, they can combine their “apples” and count the total. |
| Michael has 7 pencils. He gives 2 pencils to Sarah. How many pencils does Michael have now? | One student (“Michael”) holds 7 pencils, the other (“Sarah”) holds 2 pencils. The student playing Michael gives 2 pencils to the student playing Sarah. Then the students count how many pencils Michael is left holding. |
3. Work backwards
Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution. This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.
For example,
To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71. Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.
4. Write a number sentence
When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved. It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.
5. Use a formula
Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve. Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.
Strategies for checking the solution
Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense.
There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.
Here are five strategies to help students check their solutions.
1. Use the Inverse Operation
For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work.
2. Estimate to check for reasonableness
Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable. Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten. For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10. When the estimate is clear the two numbers are close. This means your answer is reasonable.
3. Plug-In Method
This method is particularly useful for algebraic equations. Specifically when working with variables. To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.
If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓
4. Peer Review
Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly. Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills. If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.
5. Use a Calculator
A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.
Step-by-step problem-solving processes for your classroom
In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems.
Polya’s 4 steps include:
- Understand the problem
- Devise a plan
- Carry out the plan
Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall.
Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom.
Here are 5 problem-solving strategies to introduce to students and use in the classroom.
How Third Space Learning improves problem-solving
Resources .
Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking.
Explore the range of problem solving resources for 2nd to 8th grade students.
One-on-one tutoring
Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards.
Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice.
Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.
Problem-solving
Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra.
Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.
READ MORE :
- 8 Common Core math examples
- Tier 3 Interventions: A School Leaders Guide
- Tier 2 Interventions: A School Leaders Guide
- Tier 1 Interventions: A School Leaders Guide
There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model • act it out • work backwards • write a number sentence • use a formula
Here are 10 strategies for problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model • Act it out • Work backwards • Write a number sentence • Use a formula
1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back
Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.
Related articles
Why Student Centered Learning Is Important: A Guide For Educators
13 Effective Learning Strategies: A Guide to Using them in your Math Classroom
Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers
5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms
Ultimate Guide to Metacognition [FREE]
Looking for a summary on metacognition in relation to math teaching and learning?
Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.
Equation Solver
What do you want to calculate.
- Solve for Variable
- Practice Mode
- Step-By-Step
Example (Click to try)
How to solve your equation, solving equations video lessons.
- Solving Simple Equations
Need more problem types? Try MathPapa Algebra Calculator
 Get step-by-step solutions with MathGPTUpload a screenshot or picture of your question and get instant help from your personal ai math tutor. Click here to take a picture or select an image Drag & drop or click here to upload an image of your problem 
Problem-Solving Steps that Actually WorkUpdated: Mar 6, 2023 Whenever our students encounter problems, it can be a tricky situation. On one hand, I get super excited about the idea of my students THINKING about everything they know to solve the problem. I love watching their brains work while they access that filing cabinet in their brain of math information and pull out the information to solve a challenging problem. On the other hand, that same process can become a brick wall when it becomes too overwhelming. Students can shut down and refuse to move. They can cry and become frustrated. These same students can then begin believing they are just not good at math from this point forward. That's a lot of pressure from a simple math problem. If you haven't read Jo Boaler's Mathematical Mindsets, I strongly suggest it as a way to begin helping our students see math learning with a growth mindset. It's a helpful guide in teaching our students and ourselves that knowledge is something that grows and is not fixed. It is based on Carol Dweck's work with Growth Mindsets from Mindset: The New Psychology of Success . (Another great read in helping children as a parent, teacher or coach.) So what do we do? Instead of bombarding our students with several strategies to make problem-solving easier, I think it's important to boil it down to the basics. What strategies can I give my students that help them with all problems? What's something that's easy for them to remember and recall? What's something that would give them confidence moving forward?  Enter in Polya's Problem-Solving Method by George Polya who was known as the father of problem solving. These four steps sum up everything our students need to solve problems successfully. They are easy to remember and easy to implement. (This post does contain affiliate links.) Understand the Problem: This is the focus on comprehension. What is the problem asking me to do? What do I know from reading the problem? What can I comprehend? Plan: This is the time where students think about how they want to move forward. Before solving with mathematics, we want our students to determine what steps they should take. Solve : This is where students do the math. They follow the steps in their plan and work out the problem. Look Back: Now we want students to look back and see that their answer makes sense. We want them to check the answer using estimation or even by trying to solve it in another way. Four steps...that's totally manageable right? I love the simplicity of it all and even find that it carries over to all aspects of our life when solving real-life problems. Now that students have a way to solve problems, it's time to give them the tools to make a plan that will work. I've been talking about Singapore's heuristics in my Member's Facebook group, and I wanted to share some of those with you. Stay tuned in the next few weeks to learn about the heuristics and how these strategies help students determine a meaningful plan to solve problems. In the meantime, be sure to grab your problem-solving poster by clicking below!
Recent PostsGreat Big List of Math Literature Math Literature: Goodnight Numbers and a Digital Freebie Math Literature: The Action of Subtraction Thanks for submitting! Homework Q&A Drag image here or click to upload
 Math AI SolverUse our AI math solver to solve any math homework problem online for free  Tackle Your Math Homework with Our AI Math SolverStruggling to do your math homework? HIX Tutor’s AI Math Solver simplifies math problems. Get fast, accurate math solutions in one click with our state-of-the-art math AI solver. Why Use HIX Tutor’s Math AI Homework SolverComprehensive support. Math AI Solver can assist with math at all grade levels, ranging from elementary math to university and beyond. Step-by-Step SolutionsGet detailed explanations for each step of the problem to gain a better understanding of your math homework. 24/7 AvailabilityAccess our AI math solver anytime to meet your homework needs around the clock to ensure that you never miss a deadline. Save Time and MoneyGet answers to math problems in record time and save on the cost of math tutors with our free math AI solver tool. Technologically AdvancedWe offer the latest in AI math technology to ensure accurate answers to any math problems including algebra, geometry, calculus, etc. Streamlined LearningOur AI math problem solvers make learning all kinds of math easier by providing step-by-step guidance and answers. Experience the Best Math AI Solver on the MarketStuck on a difficult math question? Math AI Solver is here to assist you: Submit Your Math QueryType in your math question or upload the document or an image of the homework problem. Let Math AI Solver Do Its MagicWait just a few moments while our advanced math homework AI tool analyzes the question and prepares an accurate solution. Receive the Correct AnswerReceive a detailed, step-by-step solution to your math query that includes an accurate answer. Other AI Homework HelpersDemystify topics ranging from basic mechanics to advanced electromagnetism with detailed solutions Chemistry AIHIX Tutor's AI chemistry homework helper is your go-to companion to master chemistry problem-solving. Clarify doubts, and get insights on complex processes and terminologies. Get accurate answers to hard. HIX Tutor’s AI Math Problem Solver Features at a Glance
1. What is Math AI?A Math AI is an artificial intelligence-powered tool designed to solve complex mathematical problems efficiently and accurately. By utilizing advanced algorithms and computational power, Math AI can provide step-by-step solutions, offer insights into problem-solving strategies, and enhance our overall understanding of various mathematical concepts. 2. What math subjects does the AI math problem solver cover?Our AI math solver tool is trained to solve a wide range of math subjects, including but not limited to, algebra, geometry, calculus, trigonometry, calculus, and more. 3. How long does this math AI take to get an answer to my math question?HIX Tutor's math AI Solver is available 24/7 and delivers correct, step-by-step solutions to maths questions almost immediately after you submit the query. 4. What's the best Math AI solver?HIX Tutor is the best Math AI that offers comprehensive solutions for solving complex mathematical problems. With its advanced features, such as step-by-step explanations, personalized learning paths, and interactive problem-solving tools, HIX Tutor aims to help students and professionals better understand mathematical concepts and improve their problem-solving skills. 5. How does HIX Tutor's AI for maths work?HIX Tutor's math AI helper utilizes advanced algorithms and deep learning techniques to analyze and understand math problems. It breaks down the problem into steps, applies relevant mathematical concepts, and provides detailed explanations for each step of the solution. 6. Is HIX Tutor's mathematics AI solver accurate?Yes, our math AI solving tool is designed to deliver accurate solutions. It has been trained on a vast dataset of mathematical problems to ensure its proficiency in providing reliable answers. However, it's important to note that while our tool strives for accuracy, occasional errors or misunderstandings may occur. 7. Is HIX Tutor's math AI solver replace the need for a maths tutor?While our maths AI tool is designed to provide comprehensive support and step-by-step solutions, it is not intended to replace the guidance and expertise of a human maths tutor. It can be a valuable tool to supplement your learning and provide quick answers, but for in-depth understanding and tailored guidance, a maths tutor may still be beneficial in certain situations. 8. Is this math AI free to use?Yes, you can try Math AI Solver at no cost. Once you’ve reached your free question limit, you’ll need to purchase an affordable subscription. Discover Frequently Asked Math Questions and Their Answers
 Trust HIX Tutor’s Math AI for Reliable Math SolutionsDon’t waste hours slaving over complex equations or confusing mathematical word problems. Math AI Solver is the ultimate solution for completing math assessments quickly and efficiently. Get started now. Game CentralTeaching Problem Solving in Math
Every year my students can be fantastic at math…until they start to see math with words. For some reason, once math gets translated into reading, even my best readers start to panic. There is just something about word problems, or problem-solving, that causes children to think they don’t know how to complete them. Every year in math, I start off by teaching my students problem-solving skills and strategies. Every year they moan and groan that they know them. Every year – paragraph one above. It was a vicious cycle. I needed something new.  I put together a problem-solving unit that would focus a bit more on strategies and steps in hopes that that would create problem-solving stars. The Problem Solving StrategiesFirst, I wanted to make sure my students all learned the different strategies to solve problems, such as guess-and-check, using visuals (draw a picture, act it out, and modeling it), working backward, and organizational methods (tables, charts, and lists). In the past, I had used worksheet pages that would introduce one and provide the students with plenty of problems practicing that one strategy. I did like that because students could focus more on practicing the strategy itself, but I also wanted students to know when to use it, too, so I made sure they had both to practice. I provided students with plenty of practice of the strategies, such as in this guess-and-check game.  There’s also this visuals strategy wheel practice.  I also provided them with paper dolls and a variety of clothing to create an organized list to determine just how many outfits their “friend” would have.  Then, as I said above, we practiced in a variety of ways to make sure we knew exactly when to use them. I really wanted to make sure they had this down!  Anyway, after I knew they had down the various strategies and when to use them, then we went into the actual problem-solving steps. The Problem Solving StepsI wanted students to understand that when they see a story problem, it isn’t scary. Really, it’s just the equation written out in words in a real-life situation. Then, I provided them with the “keys to success.” S tep 1 – Understand the Problem. To help students understand the problem, I provided them with sample problems, and together we did five important things:
We did this over and over with example problems.  Once I felt the students had it down, we practiced it in a game of problem-solving relay. Students raced one another to see how quickly they could get down to the nitty-gritty of the word problems. We weren’t solving the problems – yet.  Then, we were on to Step 2 – Make a Plan . We talked about how this was where we were going to choose which strategy we were going to use. We also discussed how this was where we were going to figure out what operation to use. I taught the students Sheila Melton’s operation concept map.  We talked about how if you know the total and know if it is equal or not, that will determine what operation you are doing. So, we took an example problem, such as: Sheldon wants to make a cupcake for each of his 28 classmates. He can make 7 cupcakes with one box of cupcake mix. How many boxes will he need to buy? We started off by asking ourselves, “Do we know the total?” We know there are a total of 28 classmates. So, yes, we are separating. Then, we ask, “Is it equal?” Yes, he wants to make a cupcake for EACH of his classmates. So, we are dividing: 28 divided by 7 = 4. He will need to buy 4 boxes. (I actually went ahead and solved it here – which is the next step, too.) Step 3 – Solving the problem . We talked about how solving the problem involves the following:
We talked specifically about thinking strategies. Just like in reading, there are thinking strategies in math. I wanted students to be aware that sometimes when we are working on a problem, a particular strategy may not be working, and we may need to switch strategies. We also discussed that sometimes we may need to rethink the problem, to think of related content, or to even start over. We discussed these thinking strategies:
To make sure they were getting in practice utilizing these thinking strategies, I gave each group chart paper with a letter from a fellow “student” (not a real student), and they had to give advice on how to help them solve their problem using the thinking strategies above.  Finally, Step 4 – Check It. This is the step that students often miss. I wanted to emphasize just how important it is! I went over it with them, discussing that when they check their problems, they should always look for these things:
Then, I gave students practice cards. I provided them with example cards of “students” who had completed their assignments already, and I wanted them to be the teacher. They needed to check the work and make sure it was completed correctly. If it wasn’t, then they needed to tell what they missed and correct it.  To demonstrate their understanding of the entire unit, we completed an adorable lap book (my first time ever putting together one or even creating one – I was surprised how well it turned out, actually). It was a great way to put everything we discussed in there.  Once we were all done, students were officially Problem Solving S.T.A.R.S. I just reminded students frequently of this acronym. Stop – Don’t rush with any solution; just take your time and look everything over. Think – Take your time to think about the problem and solution. Act – Act on a strategy and try it out. Review – Look it over and see if you got all the parts.  Wow, you are a true trooper sticking it out in this lengthy post! To sum up the majority of what I have written here, I have some problem-solving bookmarks FREE to help you remember and to help your students!  You can grab these problem-solving bookmarks for FREE by clicking here . You can do any of these ideas without having to purchase anything. However, if you are looking to save some time and energy, then they are all found in my Math Workshop Problem Solving Unit . The unit is for grade three, but it may work for other grade levels. The practice problems are all for the early third-grade level. 
 FIND IT NOW!Check me out on tpt.  CHECK THESE OUT 5th Grade Math Workshop Growing Bundle- 9 Units Three Types of Rocks and Minerals with Rock Cycle Circle BookWant to save time? COPYRIGHT © 2016-2024. The Owl Teacher | Privacy page | Disclosure Page | Shipping | Returns/Refunds BOGO on EVERYTHING!  5 Easy Steps to Solve Any Word Problem in Math
Picture this my teacher besties. You are solving word problems in your math class and every student, yes every student knows how to solve word problems without immediately entering a state of confusion! They know how to attack the problem head-on and have a method to solve every single problem that is presented to them.  How Do You Solve Word Problems in Math?Ask yourself this, what do you think is the #1 phrase a student says as soon as they see a word problem? You guessed it, my teacher friend, I don’t know how to do this! I think the most common question I get when I’m teaching my math classes, is how do I solve this? Students see word problems and immediately enter freak-out mode! Let’s take solving word problems in the classroom and make it easier for students to SOLVE the problem!  How to Solve Word Problems Step by StepThere are so many methods that students can choose from when learning how to solve word problems. The 4 step method is the foundation for all of the methods that you will see, but what about a variation of the 4 step method that every student can do just because they get it. Students are most likely confused about how to solve word problems because they have never used a consistent method over the years. I’m all about consistency in my classroom. Fortunately, in my school district, I get to teach most of the students year after year because of how small our class sizes are. So I’m going to give you a method based on the 4 step method, that allows all students to be successful at solving word problems. Even the most unmotivated math student will learn how to solve word problems and not skip them!  Tips, Tricks, and Teaching Strategies to Solving Word Problems in MathGoing back to the 4 step method just in case you need a refresher. If you know me at all a little reminder of “oh yeah I remember that now” always helps me! 4 steps in solving word problems in math:
This 4 step method is the basis of the method I’m going to tell you all about. The problem isn’t with the method itself, it is the fact that most students see word problems and just start panicking! Why can they do an entire assignment and then see a word problem and then suddenly stop? Is there a reason why books are designed with word problems at the end? These are questions that I constantly have asked myself over the last several years. I finally got to the point where my students needed a consistent approach to solving word problems that worked every single time. The first thing I knew I needed to start doing was introducing students to word problems at the beginning of each lesson. Once students first see the word problems at the beginning of the lesson, they are less likely to be scared of them when it comes time to do it by themselves! This also will increase their confidence in the classroom. In case you missed it, I shared all about how I increase my students’ confidence in the classroom. Wonder how increasing their confidence will help keep them motivated in the classroom? So confident motivated students will see word problems that could be on their homework, any standardized test, and say I GOT THIS!  Steps to Solving Word Problems in MathematicsWe are ready to SOLVE any word problem our students are going to encounter in math class. Here are my 5 easy steps to SOLVE any word problem in math:
Do you want to learn how to implement this 5 steps problem-solving strategy into your classroom? I’m hosting a FREE workshop all about how to implement this strategy in your classroom!  I am so excited to be offering a workshop to increase students’ confidence in solving word problems. The workshop is held in my Facebook Group The Round Robin Math Community. It also will be sent straight to your inbox and you can watch it right now! If you’re interested, join today and all the details will be sent to you ASAP! I will see you there! PS. Need the SOLVE method for your bulletin board for your students’ math journals/notebooks? Check out this bulletin board resource here:  Love, Robin
 Robin CorneckiLatest posts by robin cornecki ( see all ).
 Hi, I'm Robin!I am a secondary math teacher with over 19 years of experience! If you’re a teacher looking for help with all the tips, tricks, and strategies for passing the praxis math core test, you’re in the right place! I also create engaging secondary math resources for grades 7-12! Learn more about me and how I can help you here . Let's Connect!Get my top 7 strategies. Please ensure that your password is at least 8 characters and contains each of the following:
|
IMAGES
COMMENTS
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students. The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and ...
Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem. Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and ...
Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app. ... Try Math Solver. Type a math problem. Quadratic equation { x } ^ { 2 } - 4 x - 5 = 0. Trigonometry. 4 \sin \theta \cos \theta = 2 \sin \theta. Linear equation . y = 3x + 4. Arithmetic. 699 * 533 ...
Get math help in your language. Works in Spanish, Hindi, German, and more. Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
Get accurate solutions and step-by-step explanations for algebra and other math problems with the free GeoGebra Math Solver. Enhance your problem-solving skills while learning how to solve equations on your own. Try it now!
Free math problem solver answers your algebra homework questions with step-by-step explanations. Mathway. Visit Mathway on the web. Start 7-day free trial on the app. Start 7-day free trial on the app. Download free on Amazon. Download free in Windows Store.
Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, calculus and more. ... Type a math problem. Something went wrong, please try again. Examples. Quadratic equation { x } ^ { 2 } - 4 x - 5 = 0 ...
Starting at $5.00 /month. Get step-by-step answers and hints for your math homework problems. Learn the basics, check your work, gain insight on different ways to solve problems. For chemistry, calculus, algebra, trigonometry, equation solving, basic math and more.
Cymath | Math Problem Solver with Steps | Math Solving App ... \\"Solve
An identity is an equation that is satisfied by all numbers from its replacement set. Example 1 Consider the equation 2x-1 = x+2. The replacement set here is the set of all real numbers. The equation is conditional since, for example, 1 is a member of the replacement set but not of the solution set. Example 2 Consider the equation (x-1) (x+1 ...
Step 1: Understanding the problem. We are given in the problem that there are 25 chickens and cows. All together there are 76 feet. Chickens have 2 feet and cows have 4 feet. We are trying to determine how many cows and how many chickens Mr. Jones has on his farm. Step 2: Devise a plan.
Here are five strategies to help students check their solutions. 1. Use the Inverse Operation. For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7.
3. Work on an easier problem. If there is an easier problem available that is similar to the one you are trying to solve, work on the easier problem first. Solving an easier problem that requires some of the same steps and formulas will help you to tackle the more difficult problem. [8] [9] 4.
Symbolab: equation search and math solver - solves algebra, trigonometry and calculus problems step by step
Math 100: Liberal Arts Mathematics (Saburo Matsumoto) 1: Mathematics and Problem-Solving ... Make sure you use Polya's 4 problem-solving steps. Problem Solving Strategy 2 (Using a variable to find the sum of a sequence.) Gauss's strategy for sequences: last term = (fixed number) (n -1) + first term.
How to solve your equation. To solve your equation using the Equation Solver, type in your equation like x+4=5. The solver will then show you the steps to help you learn how to solve it on your own.
Even simple math problems become easier to solve when broken down into steps. From basic additions to calculus, the process of problem solving usually takes a lot of practice before answers could come easily. As problems become more complex, it becomes even more important to understand the step-by-step process by which we solve them.
MathGPT is an ai math solver, integral calculator, derivative calculator, polynomial calculator, and more! Upload a photo and solve your math homework! NEW: Generate Video Explanations . Get step-by-step solutions with MathGPT Upload a screenshot or picture of your question and get instant help from your personal AI math tutor ... Drag & drop ...
Plan: This is the time where students think about how they want to move forward. Before solving with mathematics, we want our students to determine what steps they should take. Solve: This is where students do the math. They follow the steps in their plan and work out the problem. Look Back: Now we want students to look back and see that their ...
A Math AI is an artificial intelligence-powered tool designed to solve complex mathematical problems efficiently and accurately. By utilizing advanced algorithms and computational power, Math AI can provide step-by-step solutions, offer insights into problem-solving strategies, and enhance our overall understanding of various mathematical concepts.
Learn about algebra using our free math solver with step-by-step solutions.
Then, I provided them with the "keys to success.". Step 1 - Understand the Problem. To help students understand the problem, I provided them with sample problems, and together we did five important things: read the problem carefully. restated the problem in our own words. crossed out unimportant information.
Steps to Solving Word Problems in Mathematics. We are ready to SOLVE any word problem our students are going to encounter in math class. Here are my 5 easy steps to SOLVE any word problem in math: S - State the objective. O - Outline your plan. L - Look for Key Details - Information. V - Verify and Solve.
Free math problem solver answers your calculus homework questions with step-by-step explanations. Mathway. Visit Mathway on the web. Start 7-day free trial on the app. Start 7-day free trial on the app. Download free on Amazon. Download free in Windows Store.