lesson 25 homework module 4 grade 5

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Eureka Math Grade 5 Module 4 Lesson 25 Answer Key

Engage ny eureka math 5th grade module 4 lesson 25 answer key, eureka math grade 5 module 4 lesson 25 problem set answer key.

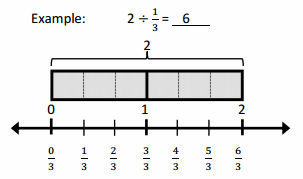
a. 4 ÷ \(\frac{1}{2}\) = _________ There are __ halves in 1 whole. There are ___ halves in 4 wholes. If 4 is \(\frac{1}{2}\), what is the whole? __

Answer: 4 ÷ \(\frac{1}{2}\) = 8 There are 2 halves in 1 whole. There are 8 halves in 4 wholes. If 4 is \(\frac{1}{2}\), the whole is 4.

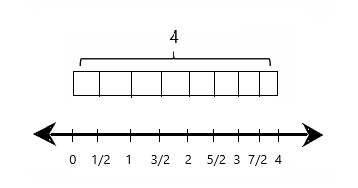
b. 2 ÷ \(\frac{1}{4}\) = __ There are ____ fourths in 1 whole. There are ____ fourths in 2 wholes. If 2 is \(\frac{1}{4}\), what is the whole? __

Answer: 2 ÷ \(\frac{1}{4}\) = 8 There are 4 fourths in 1 whole. There are 8 fourths in 2 wholes. If 2 is \(\frac{1}{4}\), the whole is 8

Explanation: Given that 2 ÷ \(\frac{1}{4}\) on solving we will get the result as 8. And there are 4 fourths in 1 whole and there are 8 fourths in 2 wholes.

c. 5 \(\frac{1}{3}\) = __ There are ____ thirds in 1 whole. There are ____ thirds in 5 wholes. If 5 is \(\frac{1}{3}\), what is the whole? __

Answer: 5 \(\frac{1}{3}\) = 15 There are 3 thirds in 1 whole. There are 15 thirds in 5 wholes. If 5 is \(\frac{1}{3}\), the whole is 15.

Explanation: Given that 5 \(\frac{1}{3}\) on solving we will get the result as 15. And there are 3 thirds in 1 whole and there are 15 thirds in 5 wholes.

d. 3 ÷ \(\frac{1}{5}\) = _________ There are ____ fifths in 1 whole. There are ____ fifths in 3 wholes. If 3 is \(\frac{1}{5}\), what is the whole? __

Answer: 3 ÷ \(\frac{1}{5}\) = 15 There are 5 fifths in 1 whole. There are 15 fifths in 3 wholes. If 3 is \(\frac{1}{5}\), the whole 15.

Explanation: Given that 3 ÷ \(\frac{1}{5}\) on solving we will get the result as 15. And there are 5 fifths in 1 whole and tThere are 15 fifths in 3 wholes.

Question 3. Divide. Then, multiply to check.

a. 5 ÷ \(\frac{1}{2}\)

Answer: 5 ÷ \(\frac{1}{2}\) = 10.

Explanation: Given that 5 ÷ \(\frac{1}{2}\) which is 5 × 2 = 10. To check we will \(\frac{1}{2}\) × 10 which is 5.

b. 3 ÷ \(\frac{1}{2}\)

Answer: 3 ÷ \(\frac{1}{2}\) = 6.

Explanation: Given that 3 ÷ \(\frac{1}{2}\) which is 3 × 2 = 6. To check we will \(\frac{1}{2}\) × 6 which is 3.

c. 4 ÷ \(\frac{1}{5}\)

Answer: 4 ÷ \(\frac{1}{5}\) = 20.

Explanation: Given that 4 ÷ \(\frac{1}{5}\) which is 4 × 5 = 20. To check we will \(\frac{1}{5}\) × 20 which is 4.

d. 1 ÷ \(\frac{1}{6}\)

Answer: 1 ÷ \(\frac{1}{6}\) = 6.

Explanation: Given that 1 ÷ \(\frac{1}{6}\) which is 1 × 6 = 6. To check we will \(\frac{1}{6}\) × 6 which is 1.

e. 2 ÷ \(\frac{1}{8}\)

Answer: 2 ÷ \(\frac{1}{8}\) = 16.

Explanation: Given that 2 ÷ \(\frac{1}{8}\) which is 2 × 8 = 16. To check we will \(\frac{1}{8}\) × 16 which is 2.

f. 7 ÷ \(\frac{1}{6}\)

Answer: 7 ÷ \(\frac{1}{6}\) = 42.

Explanation: Given that 7 ÷ \(\frac{1}{6}\) which is 7 × 6 = 42. To check we will \(\frac{1}{6}\) × 42 which is 7.

g. 8 ÷ \(\frac{1}{3}\)

Answer: 8 ÷ \(\frac{1}{3}\) = 24.

Explanation: Given that 8 ÷ \(\frac{1}{3}\) which is 8 × 3 = 24. To check we will \(\frac{1}{3}\) × 24 which is 8.

h. 9 ÷ \(\frac{1}{4}\)

Answer: 9 ÷ \(\frac{1}{4}\) = 36.

Explanation: Given that 9 ÷ \(\frac{1}{4}\) which is 9 × 4  = 36. To check we will \(\frac{1}{4}\) × 36 = 9.

Question 3. For an art project, Mrs. Williams is dividing construction paper into fourths. How many fourths can she make from 5 pieces of construction paper?

Answer: The number of fourths can she make from 5 pieces of construction paper is 20 fourths.

Explanation: Here, Mrs. Williams is dividing construction paper into fourths, so the number of fourths can she make from 5 pieces of construction paper is 5 ÷ \(\frac{1}{4}\) which is 5 × 4 = 20.

Question 4. Use the chart below to answer the following questions. Donnie’s Diner Lunch Menu

a. How many hamburgers can Donnie make with 6 pounds of hamburger meat?

Answer: The number of hamburgers can Donnie make with 6 pounds of hamburger meat is 18 hamburgers.

Explanation: The number of hamburgers can Donnie make with 6 pounds of hamburger meat is 6 ÷ \(\frac{1}{3}\) which is 6 × 3 = 18 hamburgers.

b. How many pickle servings can be made from a jar of 15 pickles?

Answer: The number of pickle servings can be made from a jar of 15 pickles is 60 pickles.

Explanation: The number of pickle servings can be made from a jar of 15 pickles is 15 ÷ \(\frac{1}{4}\) which is 15 × 4 = 60 pickles

c. How many servings of chocolate milk can he serve from a gallon of milk?

Answer: The number of servings of chocolate milk can he serve from a gallon of milk is 32 servings of chocolate milk..

Explanation: The number of servings of chocolate milk can he serve from a gallon of milk is, as 1 gallon is 16 cups and 16 ÷ \(\frac{1}{2}\) which is 16 × 2 = 32 servings of chocolate milk.

Question 5. Three gallons of water fill \(\frac{1}{4}\) of the elephant’s pail at the zoo. How much water does the pail hold?

Answer: The pail holds 12 gallons.

Explanation: Here, Three gallons of water fill \(\frac{1}{4}\) of the elephant’s pail at the zoo, so the pail holds 3 ÷ \(\frac{1}{4}\) which is 3 × 4 = 12 gallons.

Eureka Math Grade 5 Module 4 Lesson 25 Exit Ticket Answer Key

Question 1. Draw a tape diagram and a number line to solve. Fill in the blanks that follow.

a. 5 ÷ \(\frac{1}{2}\) = _________ There are ____ halves in 1 whole. There are ____ halves in 5 wholes. 5 is \(\frac{1}{2}\) of what number? _______

Answer: 5 ÷ \(\frac{1}{2}\) = 10 There are 2 halves in 1 whole. There are 10 halves in 5 wholes. 5 is \(\frac{1}{2}\) the number is 10

Explanation: Given that 5 ÷ \(\frac{1}{2}\) which is 5 × 2 = 10. And there are 2 halves in 1 whole and there are 10 halves in 5 wholes.

b. 4 ÷ \(\frac{1}{4}\) = _________ There are ____ fourths in 1 whole. There are ____ fourths in ____ wholes. 4 is \(\frac{1}{4}\) of what number? _______

Answer: 4 ÷ \(\frac{1}{4}\) = 16 There are 4 fourths in 1 whole. There are 16 fourths in 4 wholes. 4 is \(\frac{1}{4}\) the number 16

Explanation: Given that 4 ÷ \(\frac{1}{4}\) which is 4 × 4 = 16. And there are 4 fourths in 1 whole and there are 16 fourths in 4 wholes.

Question 2. Ms. Leverenz is doing an art project with her class. She has a 3 foot piece of ribbon. If she gives each student an eighth of a foot of ribbon, will she have enough for her class of 22 students?

Answer: Ms. Leverenz has 3 foot ribbon or 36 inches, so she have enough for her class 22 students.

Explanation: Here, Ms. Leverenz is doing an art project with her class and she has a 3 foot piece of ribbon, which is 12 × 3 = 36 foot. and if she gives each student an eighth of a foot of ribbon which is \(\frac{8}{12}\) = 1.5 inches of ribbon. Here Ms. Leverenz gives each students 1.5 inches ribbon. Therefore she needs for 22 students which is 22 × 1.5 = 33 inches. So she has 3 foot ribbon or 36 inches, so she have enough for her class 22 students.

Eureka Math Grade 5 Module 4 Lesson 25 Homework Answer Key

Question 1. Draw a tape diagram and a number line to solve. Fill in the blanks that follow. a. 3 ÷ \(\frac{1}{3}\) = _________ There are ____ thirds in 1 whole. There are ____ thirds in 3 wholes. If 3 is \(\frac{1}{3}\), what is the whole? _______

Answer: 3 ÷ \(\frac{1}{3}\) = 9 There are 3 thirds in 1 whole. There are 9 thirds in 3 wholes. If 3 is \(\frac{1}{3}\), the whole is 9.

Explanation: Given that 3 ÷ \(\frac{1}{3}\) which is 3 × 3 = 9. And there are 3 thirds in 1 whole and there are 9 thirds in 3 wholes.

b. 3 ÷ \(\frac{1}{4}\) = _________ There are ____ fourths in 1 whole. There are ____ fourths in __ wholes. If 3 is \(\frac{1}{4}\), what is the whole? _______

Answer: 3 ÷ \(\frac{1}{4}\) = 12 There are 4 fourths in 1 whole. There are 12 fourths in 3 wholes. If 3 is \(\frac{1}{4}\), the whole 12.

Explanation: Given that 3 ÷ \(\frac{1}{4}\) which is 3 × 4 = 12. And there are 4 fourths in 1 whole and there are 12 fourths in 3 wholes.

c. 4 ÷ \(\frac{1}{3}\) = _________ There are ____ thirds in 1 whole. There are ____ thirds in __ wholes. If 4 is \(\frac{1}{3}\), what is the whole? _______

Answer: 4 ÷ \(\frac{1}{3}\) = 12 There are 3 thirds in 1 whole. There are 12 thirds in 4 wholes. If 4 is \(\frac{1}{3}\), the whole 12.

Explanation: Given that 4 ÷ \(\frac{1}{3}\) which is 4 × 3 = 12. And there are 3 thirds in 1 whole and there are 12 thirds in 4 wholes.

d. 5 ÷ \(\frac{1}{4}\) = _________ There are ____ fourths in 1 whole. There are ____ fourths in __ wholes. If 5 is \(\frac{1}{4}\), what is the whole? _______

Answer: 5 ÷ \(\frac{1}{4}\) = 20 There are 4 fourths in 1 whole. There are 20 fourths in 5 wholes. If 5 is \(\frac{1}{4}\), the whole is 20.

Explanation: Given that 5 ÷ \(\frac{1}{4}\) which is 5 × 4 = 20. And there are 4 fourths in 1 whole and there are 20 fourths in 5 wholes.

Question 2. Divide. Then, multiply to check.

a. 2 ÷ \(\frac{1}{4}\)

Answer: 2 ÷ \(\frac{1}{4}\) = 8.

Explanation: Given that 2 ÷ \(\frac{1}{4}\) which is 2 × 4 = 8. To check we will perform multiplication \(\frac{1}{4}\) × 8 which is 2.

b. 6 ÷ \(\frac{1}{2}\)

Answer: 6 ÷ \(\frac{1}{2}\) = 12.

Explanation: Given that 6 ÷ \(\frac{1}{2}\) which is 6 × 2 = 12. To check we will perform multiplication \(\frac{1}{2}\) × 12 which is 6.

c. 5 ÷ \(\frac{1}{4}\)

Answer: 5 ÷ \(\frac{1}{4}\) = 20.

Explanation: Given that 5 ÷ \(\frac{1}{4}\) which is 5 × 4 = 20. To check we will perform multiplication \(\frac{1}{4}\) × 20 which is 5.

d. 5 ÷ \(\frac{1}{8}\)

Answer: 5 ÷ \(\frac{1}{8}\) = 40.

Explanation: Given that 5 ÷ \(\frac{1}{8}\) which is 5 × 8 = 40. To check we will perform multiplication \(\frac{1}{8}\) × 40 which is 5.

e. 6 ÷ \(\frac{1}{3}\)

Answer: 6 ÷ \(\frac{1}{3}\) = 18.

Explanation: Given that 6 ÷ \(\frac{1}{3}\) which is 6 × 3 = 18. To check we will perform multiplication \(\frac{1}{3}\) × 18 which is 6.

f. 3 ÷ \(\frac{1}{6}\)

Answer: 3 ÷ \(\frac{1}{6}\) = 18.

Explanation: Given that 3 ÷ \(\frac{1}{6}\) which is 3 × 6 = 18. To check we will perform multiplication \(\frac{1}{6}\) × 18 which is 3.

g. 6 ÷ \(\frac{1}{5}\)

Answer: 6 ÷ \(\frac{1}{5}\) = 30.

Explanation: Given that 6 ÷ \(\frac{1}{5}\) which is 6 × 5 = 30. To check we will perform multiplication \(\frac{1}{5}\) × 30 which is 6.

h. 6 ÷ \(\frac{1}{10}\)

Answer: 6 ÷ \(\frac{1}{10}\) = 60.

Explanation: Given that 6 ÷ \(\frac{1}{10}\) which is 6 × 10 = 60. To check we will perform multiplication \(\frac{1}{10}\) × 60 which is 6.

Question 3. A principal orders 8 sub sandwiches for a teachers’ meeting. She cuts the subs into thirds and puts the mini-subs onto a tray. How many mini-subs are on the tray?

Answer: There will be 24 mini-subs are on the tray.

Explanation: Given there are 8 sub sandwiches for a teachers meeting and each sandwich cuts into third. So 1 ÷ \(\frac{1}{3}\) which is 1 × 3 = 3 as there are 8 sub sandwiches, so there will be 8 × 3 = 24 mini-subs are on the tray.

Question 4. Some students prepare 3 different snacks. They make \(\frac{1}{8}\) pound bags of nut mix, \(\frac{1}{4}\) pound bags of cherries, and \(\frac{1}{6}\) pound bags of dried fruit. If they buy 3 pounds of nut mix, 5 pounds of cherries, and 4 pounds of dried fruit, how many of each type of snack bag will they be able to make?

Answer: There are 24 nut mix, 20 cherry bags and 24 dried fruits.

Explanation: As some students prepare 3 different snacks and they make \(\frac{1}{8}\) pound bags of nut mix and they will be able to make number of nut mix bag is 3 ÷ \(\frac{1}{8}\)  which is 3 × 8 = 24, and \(\frac{1}{4}\) pound bags of cherries they will be able to make number of cherries bag is 5 ÷ \(\frac{1}{4}\) which is 5 × 4 = 20 , and \(\frac{1}{6}\) pound bags of dried fruit and they will be able to make number of bags of dried fruit is 4 ÷ \(\frac{1}{6}\) which is 4 × 6 = 24. So there are 24 nut mix, 20 cherry bags and 24 dried fruits.

Leave a Comment Cancel Reply

You must be logged in to post a comment.

EMBARC.Online

Homework solutions, hw solutions: eureka math grade 5 module 4 lesson 1.

https://drive.google.com/open?id=0Bze4eU0rInwwbUViZE5mcVZZUDQ  

Please email me if there is a major mistake in the solutions. I'll fix it ASAP.

EngageNY Eureka Module 4 Lesson 25 Grade 5 Classwork

• Easel Activity Frequently assigned

Description

Classwork that follows the Eureka math lesson plan for lesson 25 of module 4 (grade 5).

Questions & Answers

Teach at your own risk by kimberly g.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think