purpose of hypothesis testing in research

• Python for Data Science
• Data Analysis
• Machine Learning
• Deep Learning
• Deep Learning Interview Questions
• ML Projects
• ML Interview Questions

Understanding Hypothesis Testing

Hypothesis testing is a fundamental statistical method employed in various fields, including data science , machine learning , and statistics , to make informed decisions based on empirical evidence. It involves formulating assumptions about population parameters using sample statistics and rigorously evaluating these assumptions against collected data. At its core, hypothesis testing is a systematic approach that allows researchers to assess the validity of a statistical claim about an unknown population parameter. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

Table of Content

What is Hypothesis Testing?

Why do we use hypothesis testing, one-tailed and two-tailed test, what are type 1 and type 2 errors in hypothesis testing, how does hypothesis testing work, real life examples of hypothesis testing, limitations of hypothesis testing.

A hypothesis is an assumption or idea, specifically a statistical claim about an unknown population parameter. For example, a judge assumes a person is innocent and verifies this by reviewing evidence and hearing testimony before reaching a verdict.

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

To test the validity of the claim or assumption about the population parameter:

• A sample is drawn from the population and analyzed.
• The results of the analysis are used to decide whether the claim is true or not.

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

This structured approach to hypothesis testing in data science , hypothesis testing in machine learning , and hypothesis testing in statistics is crucial for making informed decisions based on data.

• By employing hypothesis testing in data analytics and other fields, practitioners can rigorously evaluate their assumptions and derive meaningful insights from their analyses.
• Understanding hypothesis generation and testing is also essential for effectively implementing statistical hypothesis testing in various applications.

Defining Hypotheses

• Null hypothesis (H 0 ): In statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured cases or no relationship among groups. In other words, it is a basic assumption or made based on the problem knowledge. Example : A company’s mean production is 50 units/per da H 0 : [Tex]\mu [/Tex] = 50.
• Alternative hypothesis (H 1 ): The alternative hypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis.  Example: A company’s production is not equal to 50 units/per day i.e. H 1 : [Tex]\mu [/Tex] [Tex]\ne [/Tex] 50.

Key Terms of Hypothesis Testing

• Level of significance : It refers to the degree of significance in which we accept or reject the null hypothesis. 100% accuracy is not possible for accepting a hypothesis, so we, therefore, select a level of significance that is usually 5%. This is normally denoted with  [Tex]\alpha[/Tex] and generally, it is 0.05 or 5%, which means your output should be 95% confident to give a similar kind of result in each sample.
• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.

Understanding hypothesis testing in statistics is essential for data scientists and machine learning practitioners, as it provides a structured framework for statistical hypothesis generation and testing. This methodology can also be applied in hypothesis testing in Python , enabling data analysts to perform robust statistical analyses efficiently. By employing techniques such as multiple hypothesis testing in machine learning , researchers can ensure more reliable results and avoid potential pitfalls associated with drawing conclusions from statistical tests. 

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

• Left-Tailed (Left-Sided) Test: The alternative hypothesis asserts that the true parameter value is less than the null hypothesis. Example: H 0 ​: [Tex]\mu \geq 50 [/Tex] and H 1 : [Tex]\mu < 50 [/Tex]
• Right-Tailed (Right-Sided) Test : The alternative hypothesis asserts that the true parameter value is greater than the null hypothesis. Example: H 0 : [Tex]\mu \leq50 [/Tex] and H 1 : [Tex]\mu > 50 [/Tex]

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

Example: H 0 : [Tex]\mu = [/Tex] 50 and H 1 : [Tex]\mu \neq 50 [/Tex]

To delve deeper into differences into both types of test: Refer to link

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

• Type I error: When we reject the null hypothesis, although that hypothesis was true. Type I error is denoted by alpha( [Tex]\alpha [/Tex] ).
• Type II errors : When we accept the null hypothesis, but it is false. Type II errors are denoted by beta( [Tex]\beta [/Tex] ).

Step 1: Define Null and Alternative Hypothesis

State the null hypothesis ( [Tex]H_0 [/Tex] ), representing no effect, and the alternative hypothesis ( [Tex]H_1 [/Tex] ​), suggesting an effect or difference.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Select a significance level ( [Tex]\alpha [/Tex] ), typically 0.05, to determine the threshold for rejecting the null hypothesis. It provides validity to our hypothesis test, ensuring that we have sufficient data to back up our claims. Usually, we determine our significance level beforehand of the test. The p-value is the criterion used to calculate our significance value.

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

• If the p-value is less than or equal to the significance level i.e. ( [Tex]p\leq\alpha [/Tex] ), you reject the null hypothesis. This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis.
• If the p-value is greater than the significance level i.e. ( [Tex]p\geq \alpha[/Tex] ), you fail to reject the null hypothesis. This suggests that the observed results are consistent with what would be expected under the null hypothesis.

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

[Tex]z = \frac{\bar{x} – \mu}{\frac{\sigma}{\sqrt{n}}}[/Tex]

• [Tex]\bar{x} [/Tex] is the sample mean,
• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

[Tex]t=\frac{x̄-μ}{s/\sqrt{n}} [/Tex]

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

[Tex]\chi^2 = \sum \frac{(O_{ij} – E_{ij})^2}{E_{ij}}[/Tex]

• [Tex]O_{ij}[/Tex] is the observed frequency in cell [Tex]{ij} [/Tex]
• i,j are the rows and columns index respectively.
• [Tex]E_{ij}[/Tex] is the expected frequency in cell [Tex]{ij}[/Tex] , calculated as : [Tex]\frac{{\text{{Row total}} \times \text{{Column total}}}}{{\text{{Total observations}}}}[/Tex]

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Case A

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

T-statistic (from scipy): -9.0 P-value (from scipy): 8.538051223166285e-06 T-statistic (calculated manually): -9.0 Decision: Reject the null hypothesis at alpha=0.05. Conclusion: There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

The test statistic is calculated by using the z formula Z = [Tex](203.8 – 200) / (5 \div \sqrt{25}) [/Tex] ​ and we get accordingly , Z =2.039999999999992.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Python Implementation of Case B

Reject the null hypothesis. There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL.

Although hypothesis testing is a useful technique in data science , it does not offer a comprehensive grasp of the topic being studied.

• Lack of Comprehensive Insight : Hypothesis testing in data science often focuses on specific hypotheses, which may not fully capture the complexity of the phenomena being studied.
• Dependence on Data Quality : The accuracy of hypothesis testing results relies heavily on the quality of available data. Inaccurate data can lead to incorrect conclusions, particularly in hypothesis testing in machine learning .
• Overlooking Patterns : Sole reliance on hypothesis testing can result in the omission of significant patterns or relationships in the data that are not captured by the tested hypotheses.
• Contextual Limitations : Hypothesis testing in statistics may not reflect the broader context, leading to oversimplification of results.
• Complementary Methods Needed : To gain a more holistic understanding, it’s essential to complement hypothesis testing with other analytical approaches, especially in data analytics and data mining .
• Misinterpretation Risks : Poorly formulated hypotheses or inappropriate statistical methods can lead to misinterpretation, emphasizing the need for careful consideration in hypothesis testing in Python and related analyses.
• Multiple Hypothesis Testing Challenges : Multiple hypothesis testing in machine learning poses additional challenges, as it can increase the likelihood of Type I errors, requiring adjustments to maintain validity.

Hypothesis testing is a cornerstone of statistical analysis , allowing data scientists to navigate uncertainties and draw credible inferences from sample data. By defining null and alternative hypotheses, selecting significance levels, and employing statistical tests, researchers can validate their assumptions effectively.

This article emphasizes the distinction between Type I and Type II errors, highlighting their relevance in hypothesis testing in data science and machine learning . A practical example involving a paired T-test to assess a new drug’s effect on blood pressure underscores the importance of statistical rigor in data-driven decision-making .

Ultimately, understanding hypothesis testing in statistics , alongside its applications in data mining , data analytics , and hypothesis testing in Python , enhances analytical frameworks and supports informed decision-making.

Understanding Hypothesis Testing- FAQs

What is hypothesis testing in data science.

In data science, hypothesis testing is used to validate assumptions or claims about data. It helps data scientists determine whether observed patterns are statistically significant or could have occurred by chance.

How does hypothesis testing work in machine learning?

In machine learning, hypothesis testing helps assess the effectiveness of models. For example, it can be used to compare the performance of different algorithms or to evaluate whether a new feature significantly improves a model’s accuracy.

What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

What is the difference between hypothesis testing and data mining?

Hypothesis testing focuses on evaluating specific claims or hypotheses about a dataset, while data mining involves exploring large datasets to discover patterns, relationships, or insights without predefined hypotheses.

How is hypothesis generation used in business analytics?

In business analytics , hypothesis generation involves formulating assumptions or predictions based on available data. These hypotheses can then be tested using statistical methods to inform decision-making and strategy.

What is the significance level in hypothesis testing?

The significance level, often denoted as alpha (α), is the threshold for deciding whether to reject the null hypothesis. Common significance levels are 0.05, 0.01, and 0.10, indicating the probability of making a Type I error in statistical hypothesis testing .

Similar Reads

• Data Science
• data-science

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Hypothesis tests

• Author information
• Article notes
• Copyright and License information

Accepted 2019 Mar 28; Issue date 2019 Jul.

Key points.

Hypothesis tests are used to assess whether a difference between two samples represents a real difference between the populations from which the samples were taken.

A null hypothesis of ‘no difference’ is taken as a starting point, and we calculate the probability that both sets of data came from the same population. This probability is expressed as a p -value.

When the null hypothesis is false, p- values tend to be small. When the null hypothesis is true, any p- value is equally likely.

Learning objectives.

By reading this article, you should be able to:

Explain why hypothesis testing is used.

Use a table to determine which hypothesis test should be used for a particular situation.

Interpret a p- value.

A hypothesis test is a procedure used in statistics to assess whether a particular viewpoint is likely to be true. They follow a strict protocol, and they generate a ‘ p- value’, on the basis of which a decision is made about the truth of the hypothesis under investigation. All of the routine statistical ‘tests’ used in research— t- tests, χ 2 tests, Mann–Whitney tests, etc.—are all hypothesis tests, and in spite of their differences they are all used in essentially the same way. But why do we use them at all?

Comparing the heights of two individuals is easy: we can measure their height in a standardised way and compare them. When we want to compare the heights of two small well-defined groups (for example two groups of children), we need to use a summary statistic that we can calculate for each group. Such summaries (means, medians, etc.) form the basis of descriptive statistics, and are well described elsewhere. 1 However, a problem arises when we try to compare very large groups or populations: it may be impractical or even impossible to take a measurement from everyone in the population, and by the time you do so, the population itself will have changed. A similar problem arises when we try to describe the effects of drugs—for example by how much on average does a particular vasopressor increase MAP?

To solve this problem, we use random samples to estimate values for populations. By convention, the values we calculate from samples are referred to as statistics and denoted by Latin letters ( x ¯ for sample mean; SD for sample standard deviation) while the unknown population values are called parameters , and denoted by Greek letters (μ for population mean, σ for population standard deviation).

Inferential statistics describes the methods we use to estimate population parameters from random samples; how we can quantify the level of inaccuracy in a sample statistic; and how we can go on to use these estimates to compare populations.

Sampling error

There are many reasons why a sample may give an inaccurate picture of the population it represents: it may be biased, it may not be big enough, and it may not be truly random. However, even if we have been careful to avoid these pitfalls, there is an inherent difference between the sample and the population at large. To illustrate this, let us imagine that the actual average height of males in London is 174 cm. If I were to sample 100 male Londoners and take a mean of their heights, I would be very unlikely to get exactly 174 cm. Furthermore, if somebody else were to perform the same exercise, it would be unlikely that they would get the same answer as I did. The sample mean is different each time it is taken, and the way it differs from the actual mean of the population is described by the standard error of the mean (standard error, or SEM ). The standard error is larger if there is a lot of variation in the population, and becomes smaller as the sample size increases. It is calculated thus:

where SD is the sample standard deviation, and n is the sample size.

As errors are normally distributed, we can use this to estimate a 95% confidence interval on our sample mean as follows:

We can interpret this as meaning ‘We are 95% confident that the actual mean is within this range.’

Some confusion arises at this point between the SD and the standard error. The SD is a measure of variation in the sample. The range x ¯ ± ( 1.96 × SD ) will normally contain 95% of all your data. It can be used to illustrate the spread of the data and shows what values are likely. In contrast, standard error tells you about the precision of the mean and is used to calculate confidence intervals.

One straightforward way to compare two samples is to use confidence intervals. If we calculate the mean height of two groups and find that the 95% confidence intervals do not overlap, this can be taken as evidence of a difference between the two means. This method of statistical inference is reasonably intuitive and can be used in many situations. 2 Many journals, however, prefer to report inferential statistics using p -values.

Inference testing using a null hypothesis

In 1925, the British statistician R.A. Fisher described a technique for comparing groups using a null hypothesis , a method which has dominated statistical comparison ever since. The technique itself is rather straightforward, but often gets lost in the mechanics of how it is done. To illustrate, imagine we want to compare the HR of two different groups of people. We take a random sample from each group, which we call our data. Then:

Assume that both samples came from the same group. This is our ‘null hypothesis’.

Calculate the probability that an experiment would give us these data, assuming that the null hypothesis is true. We express this probability as a p- value, a number between 0 and 1, where 0 is ‘impossible’ and 1 is ‘certain’.

If the probability of the data is low, we reject the null hypothesis and conclude that there must be a difference between the two groups.

Formally, we can define a p- value as ‘the probability of finding the observed result or a more extreme result, if the null hypothesis were true.’ Standard practice is to set a cut-off at p <0.05 (this cut-off is termed the alpha value). If the null hypothesis were true, a result such as this would only occur 5% of the time or less; this in turn would indicate that the null hypothesis itself is unlikely. Fisher described the process as follows: ‘Set a low standard of significance at the 5 per cent point, and ignore entirely all results which fail to reach this level. A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance.’ 3 This probably remains the most succinct description of the procedure.

A question which often arises at this point is ‘Why do we use a null hypothesis?’ The simple answer is that it is easy: we can readily describe what we would expect of our data under a null hypothesis, we know how data would behave, and we can readily work out the probability of getting the result that we did. It therefore makes a very simple starting point for our probability assessment. All probabilities require a set of starting conditions, in much the same way that measuring the distance to London needs a starting point. The null hypothesis can be thought of as an easy place to put the start of your ruler.

If a null hypothesis is rejected, an alternate hypothesis must be adopted in its place. The null and alternate hypotheses must be mutually exclusive, but must also between them describe all situations. If a null hypothesis is ‘no difference exists’ then the alternate should be simply ‘a difference exists’.

Hypothesis testing in practice

The components of a hypothesis test can be readily described using the acronym GOST: identify the Groups you wish to compare; define the Outcome to be measured; collect and Summarise the data; then evaluate the likelihood of the null hypothesis, using a Test statistic .

When considering groups, think first about how many. Is there just one group being compared against an audit standard, or are you comparing one group with another? Some studies may wish to compare more than two groups. Another situation may involve a single group measured at different points in time, for example before or after a particular treatment. In this situation each participant is compared with themselves, and this is often referred to as a ‘paired’ or a ‘repeated measures’ design. It is possible to combine these types of groups—for example a researcher may measure arterial BP on a number of different occasions in five different groups of patients. Such studies can be difficult, both to analyse and interpret.

In other studies we may want to see how a continuous variable (such as age or height) affects the outcomes. These techniques involve regression analysis, and are beyond the scope of this article.

The outcome measures are the data being collected. This may be a continuous measure, such as temperature or BMI, or it may be a categorical measure, such as ASA status or surgical specialty. Often, inexperienced researchers will strive to collect lots of outcome measures in an attempt to find something that differs between the groups of interest; if this is done, a ‘primary outcome measure’ should be identified before the research begins. In addition, the results of any hypothesis tests will need to be corrected for multiple measures.

The summary and the test statistic will be defined by the type of data that have been collected. The test statistic is calculated then transformed into a p- value using tables or software. It is worth looking at two common tests in a little more detail: the χ 2 test, and the t -test.

Categorical data: the χ 2 test

The χ 2 test of independence is a test for comparing categorical outcomes in two or more groups. For example, a number of trials have compared surgical site infections in patients who have been given different concentrations of oxygen perioperatively. In the PROXI trial, 4 685 patients received oxygen 80%, and 701 patients received oxygen 30%. In the 80% group there were 131 infections, while in the 30% group there were 141 infections. In this study, the groups were oxygen 80% and oxygen 30%, and the outcome measure was the presence of a surgical site infection.

The summary is a table ( Table 1 ), and the hypothesis test compares this table (the ‘observed’ table) with the table that would be expected if the proportion of infections in each group was the same (the ‘expected’ table). The test statistic is χ 2 , from which a p- value is calculated. In this instance the p -value is 0.64, which means that results like this would occur 64% of the time if the null hypothesis were true. We thus have no evidence to reject the null hypothesis; the observed difference probably results from sampling variation rather than from an inherent difference between the two groups.

Summary of the results of the PROXI trial. Figures are numbers of patients.

Continuous data: the t- test

The t- test is a statistical method for comparing means, and is one of the most widely used hypothesis tests. Imagine a study where we try to see if there is a difference in the onset time of a new neuromuscular blocking agent compared with suxamethonium. We could enlist 100 volunteers, give them a general anaesthetic, and randomise 50 of them to receive the new drug and 50 of them to receive suxamethonium. We then time how long it takes (in seconds) to have ideal intubation conditions, as measured by a quantitative nerve stimulator. Our data are therefore a list of times. In this case, the groups are ‘new drug’ and suxamethonium, and the outcome is time, measured in seconds. This can be summarised by using means; the hypothesis test will compare the means of the two groups, using a p- value calculated from a ‘ t statistic’. Hopefully it is becoming obvious at this point that the test statistic is usually identified by a letter, and this letter is often cited in the name of the test.

The t -test comes in a number of guises, depending on the comparison being made. A single sample can be compared with a standard (Is the BMI of school leavers in this town different from the national average?); two samples can be compared with each other, as in the example above; or the same study subjects can be measured at two different times. The latter case is referred to as a paired t- test, because each participant provides a pair of measurements—such as in a pre- or postintervention study.

A large number of methods for testing hypotheses exist; the commonest ones and their uses are described in Table 2 . In each case, the test can be described by detailing the groups being compared ( Table 2 , columns) the outcome measures (rows), the summary, and the test statistic. The decision to use a particular test or method should be made during the planning stages of a trial or experiment. At this stage, an estimate needs to be made of how many test subjects will be needed. Such calculations are described in detail elsewhere. 5

The principle types of hypothesis test. Tests comparing more than two samples can indicate that one group differs from the others, but will not identify which. Subsequent ‘post hoc’ testing is required if a difference is found.

Controversies surrounding hypothesis testing

Although hypothesis tests have been the basis of modern science since the middle of the 20th century, they have been plagued by misconceptions from the outset; this has led to what has been described as a crisis in science in the last few years: some journals have gone so far as to ban p -value s outright. 6 This is not because of any flaw in the concept of a p -value, but because of a lack of understanding of what they mean.

Possibly the most pervasive misunderstanding is the belief that the p- value is the chance that the null hypothesis is true, or that the p- value represents the frequency with which you will be wrong if you reject the null hypothesis (i.e. claim to have found a difference). This interpretation has frequently made it into the literature, and is a very easy trap to fall into when discussing hypothesis tests. To avoid this, it is important to remember that the p- value is telling us something about our sample , not about the null hypothesis. Put in simple terms, we would like to know the probability that the null hypothesis is true, given our data. The p- value tells us the probability of getting these data if the null hypothesis were true, which is not the same thing. This fallacy is referred to as ‘flipping the conditional’; the probability of an outcome under certain conditions is not the same as the probability of those conditions given that the outcome has happened.

A useful example is to imagine a magic trick in which you select a card from a normal deck of 52 cards, and the performer reveals your chosen card in a surprising manner. If the performer were relying purely on chance, this would only happen on average once in every 52 attempts. On the basis of this, we conclude that it is unlikely that the magician is simply relying on chance. Although simple, we have just performed an entire hypothesis test. We have declared a null hypothesis (the performer was relying on chance); we have even calculated a p -value (1 in 52, ≈0.02); and on the basis of this low p- value we have rejected our null hypothesis. We would, however, be wrong to suggest that there is a probability of 0.02 that the performer is relying on chance—that is not what our figure of 0.02 is telling us.

To explore this further we can create two populations, and watch what happens when we use simulation to take repeated samples to compare these populations. Computers allow us to do this repeatedly, and to see what p- value s are generated (see Supplementary online material). 7 Fig 1 illustrates the results of 100,000 simulated t -tests, generated in two set of circumstances. In Fig 1 a , we have a situation in which there is a difference between the two populations. The p- value s cluster below the 0.05 cut-off, although there is a small proportion with p >0.05. Interestingly, the proportion of comparisons where p <0.05 is 0.8 or 80%, which is the power of the study (the sample size was specifically calculated to give a power of 80%).

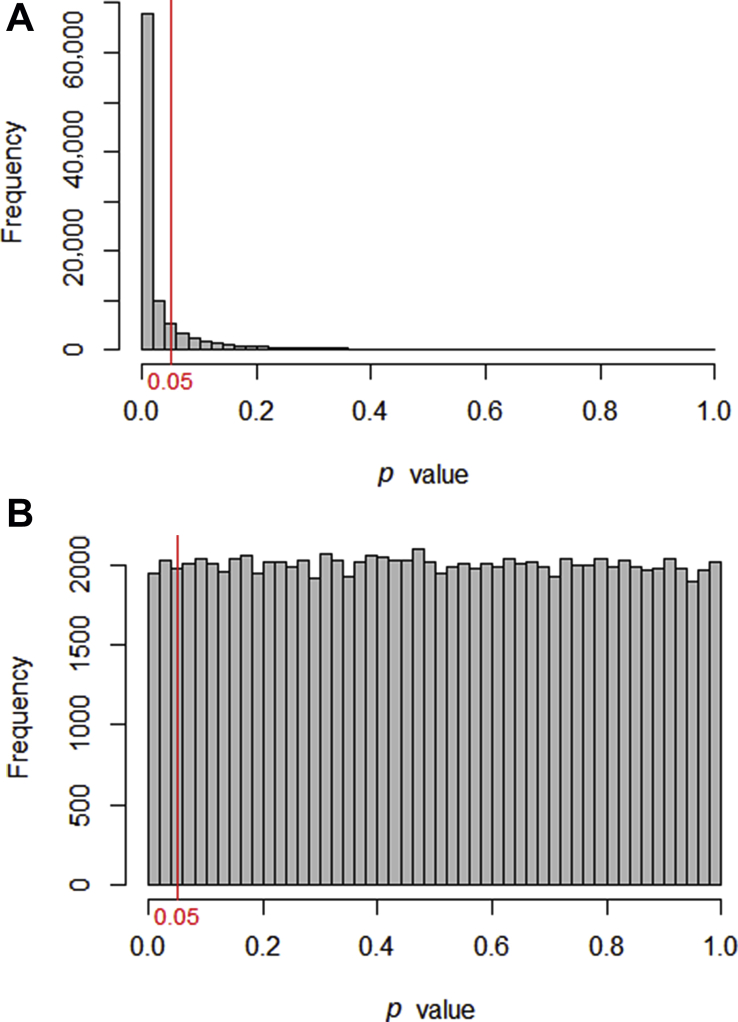
The p- value s generated when 100,000 t -tests are used to compare two samples taken from defined populations. ( a ) The populations have a difference and the p- value s are mostly significant. ( b ) The samples were taken from the same population (i.e. the null hypothesis is true) and the p- value s are distributed uniformly.

Figure 1 b depicts the situation where repeated samples are taken from the same parent population (i.e. the null hypothesis is true). Somewhat surprisingly, all p- value s occur with equal frequency, with p <0.05 occurring exactly 5% of the time. Thus, when the null hypothesis is true, a type I error will occur with a frequency equal to the alpha significance cut-off.

Figure 1 highlights the underlying problem: when presented with a p -value <0.05, is it possible with no further information, to determine whether you are looking at something from Fig 1 a or Fig 1 b ?

Finally, it cannot be stressed enough that although hypothesis testing identifies whether or not a difference is likely, it is up to us as clinicians to decide whether or not a statistically significant difference is also significant clinically.

Hypothesis testing: what next?

As mentioned above, some have suggested moving away from p -values, but it is not entirely clear what we should use instead. Some sources have advocated focussing more on effect size; however, without a measure of significance we have merely returned to our original problem: how do we know that our difference is not just a result of sampling variation?

One solution is to use Bayesian statistics. Up until very recently, these techniques have been considered both too difficult and not sufficiently rigorous. However, recent advances in computing have led to the development of Bayesian equivalents of a number of standard hypothesis tests. 8 These generate a ‘Bayes Factor’ (BF), which tells us how more (or less) likely the alternative hypothesis is after our experiment. A BF of 1.0 indicates that the likelihood of the alternate hypothesis has not changed. A BF of 10 indicates that the alternate hypothesis is 10 times more likely than we originally thought. A number of classifications for BF exist; greater than 10 can be considered ‘strong evidence’, while BF greater than 100 can be classed as ‘decisive’.

Figures such as the BF can be quoted in conjunction with the traditional p- value, but it remains to be seen whether they will become mainstream.

Declaration of interest

The author declares that they have no conflict of interest.

The associated MCQs (to support CME/CPD activity) will be accessible at www.bjaed.org/cme/home by subscribers to BJA Education .

Jason Walker FRCA FRSS BSc (Hons) Math Stat is a consultant anaesthetist at Ysbyty Gwynedd Hospital, Bangor, Wales, and an honorary senior lecturer at Bangor University. He is vice chair of his local research ethics committee, and an examiner for the Primary FRCA.

Matrix codes: 1A03, 2A04, 3J03

Supplementary data to this article can be found online at https://doi.org/10.1016/j.bjae.2019.03.006 .

Supplementary material

The following is the Supplementary data to this article:

• 1. McCluskey A., Lalkhen A.G. Statistics II: central tendency and spread of data. CEACCP. 2007;7:127–130. [ Google Scholar ]
• 2. Altman D.G., Machin D., Bryant T.N., Gardner M.J. 2nd Edn. BMJ Books; London: 2000. Statistics with confidence. [ Google Scholar ]
• 3. Fisher R.A. The arrangement of field experiments. J Min Agric Gr Br. 1926;33:503–513. [ Google Scholar ]
• 4. Meyhoff C.S., Wetterslev J., Jorgensen L.N. Effect of high perioperative oxygen fraction on surgical site infection and pulmonary complications after abdominal surgery: the PROXI randomized clinical trial. JAMA. 2009;302:1543–1550. doi: 10.1001/jama.2009.1452. [ DOI ] [ PubMed ] [ Google Scholar ]
• 5. Columb M.O., Atkinson M.S. Statistical analysis: sample size and power estimations. BJA Educ. 2016;16:159–161. [ Google Scholar ]
• 6. Trafimow D., Marks M. Editorial. Basic Appl Soc Psych. 2015;37:1–2. [ Google Scholar ]
• 7. Colquhoun D. An investigation of the false discovery rate and the misinterpretation of p-values. R Soc Open Sci. 2014;1:140216. doi: 10.1098/rsos.140216. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 8. Ly A., Verhagen J., Wagenmakers E. Harold Jeffreys’s default Bayes factor hypothesis tests: explanation, extension, and application in psychology. J Math Psychol. 2016;72:19–32. [ Google Scholar ]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

• View on publisher site
• PDF (344.3 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections